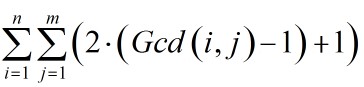题目链接：

题意：给定n和m，求

思路：本题主要是解决对于给定的t，有多少对(i,j)满足x=Gcd(i,j)。有多少对呢？我们先求出有多少对的约数为x，有(n/x)*(m/x)种！那么接着就是减去约数大于x的对数。设a[x]表示Gcd为x的对数，我们现在求出的约数为x的对数，那么显然a[x]=a[x]-a[2*x]-a[3*x]-a[4*x]。。注意这里求的时候要倒着枚举x。

int n,m;

i64 a[N];

int main()

{

    RD(n,m);

    int x=min(n,m),i,j;

    FOR1(i,x) a[i]=(i64)(n/i)*(m/i);

    for(i=x;i>=1;i--) for(j=2;j*i<=x;j++) a[i]-=a[j*i];

    i64 ans=0;

    FOR1(i,x) ans+=(2*(i-1)+1)*a[i];

    PR(ans);

}